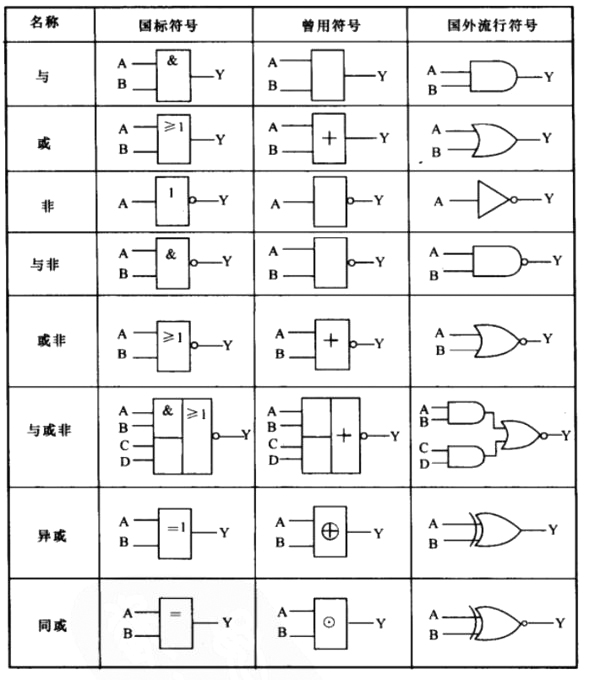
与 AND
一个逻辑命题的所有条件(输入)同时成立时,结论(输出)才成立。
与 的逻辑表达式:X=A·B=AB
可以读成 A与B ,也可以读成 A乘B,乘号也可以省略 【·不代表乘法,它代表AND运算】
与 的符号:
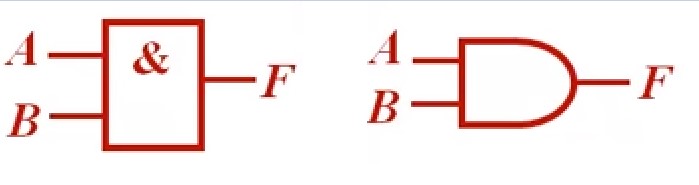
左边是矩形轮廓符号(国标符号),右边是特定外形符号(国外流行符号)
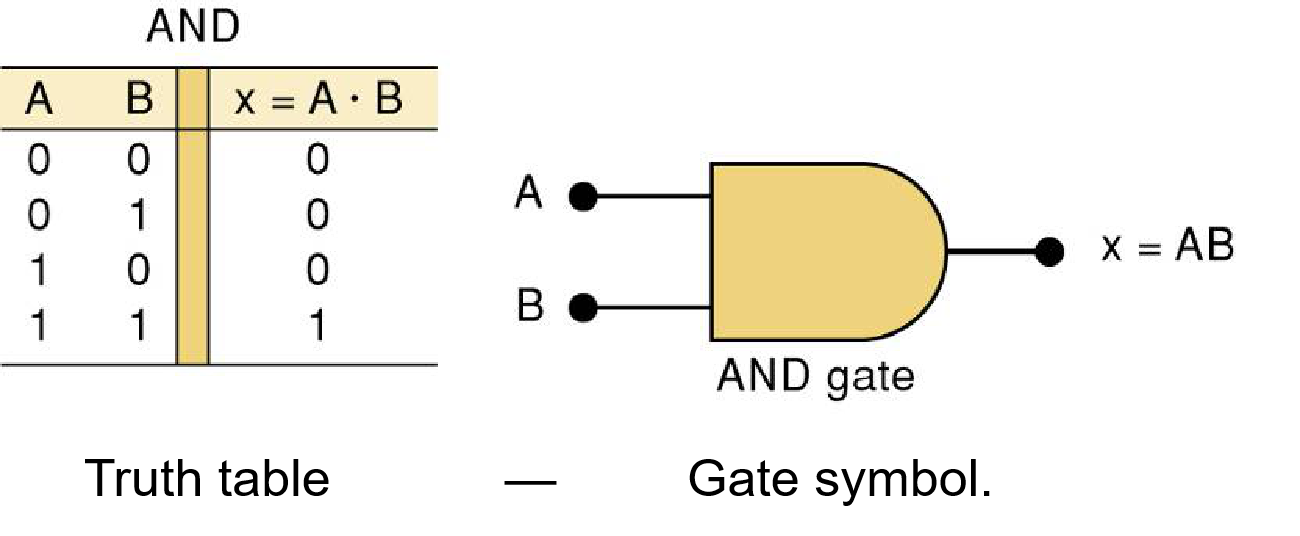
与 的真值表
两输入:
三输入:
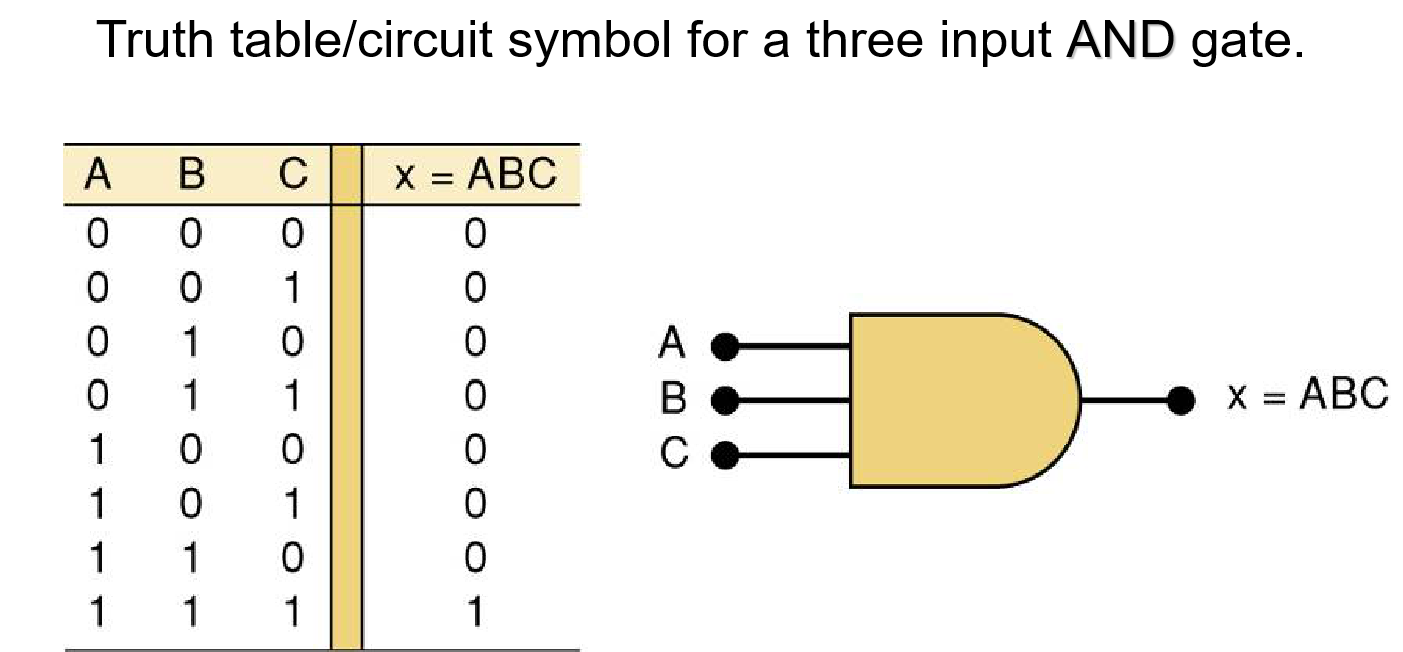
在逻辑电路图中 AND 只有当所有输入为HIGH时,输出才为HIGH
有0就是0,全1才是1
或 OR
一个逻辑命题的所有条件(输入)中,只要有一个成立,结论(输出)就成立。
或 的逻辑表达式:X=A+B
可以读成 A加B ,也可以读成 A或B【加不代表加法,它代表or运算】
当表达式中A和B等于1的时候 1+1=1 也不是1+1=2
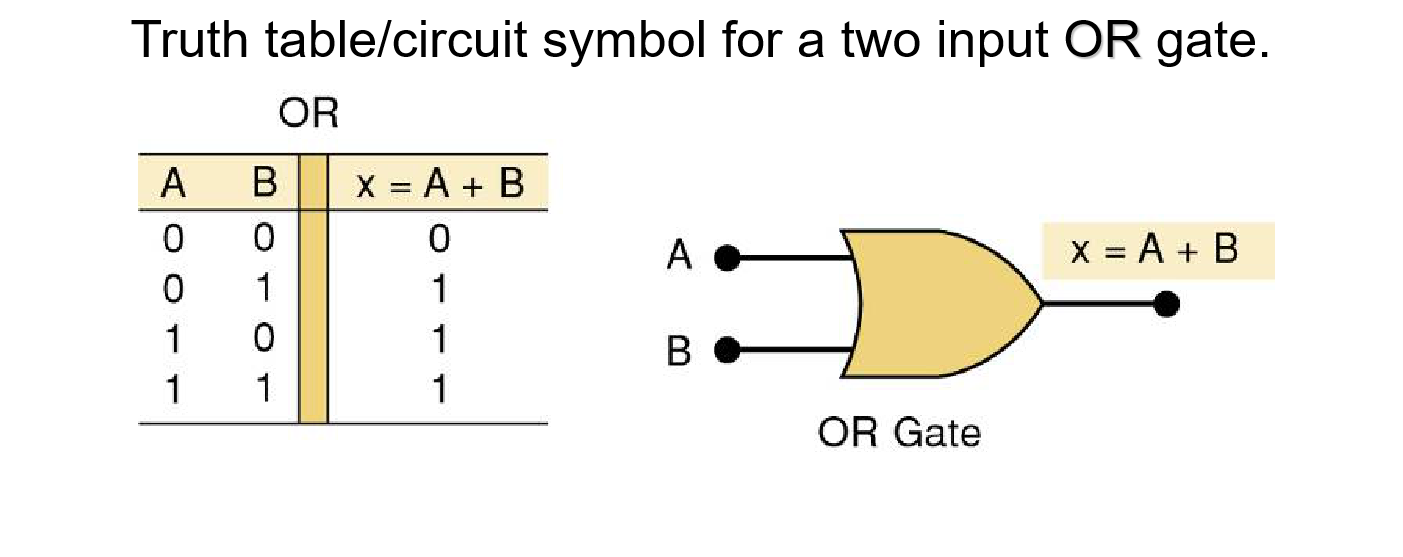
或 的符号:
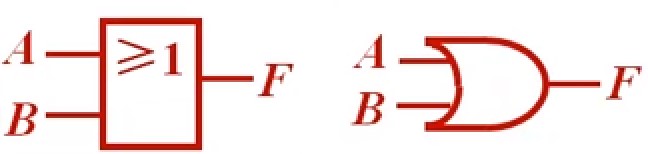
左边是矩形轮廓符号(国标符号),右边是特定外形符号(国外流行符号)
或 的真值表(两输入和三输入)
两输入:
三输入:
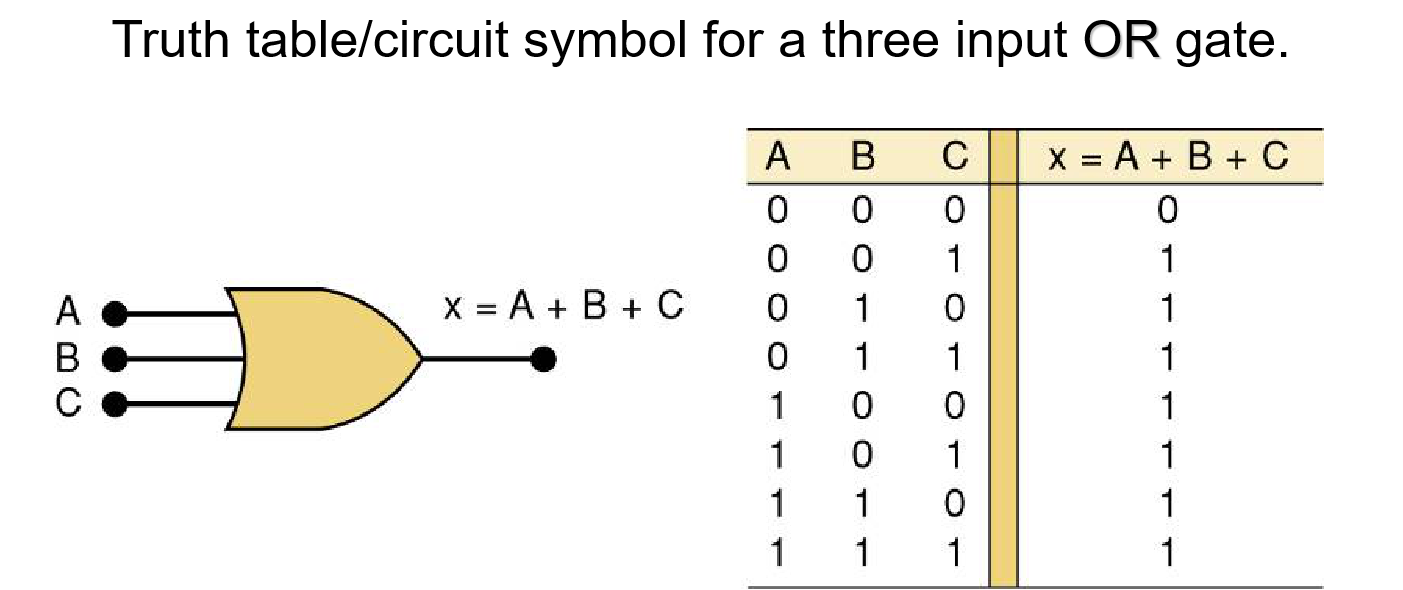
在逻辑电路图中OR 只要有一个输入为HIGH时,输出就为HIGH
遇1得1,全0得0
非 NOT
逻辑命题的条件不成立时,结论必成立;条件成立时,结论必不成立。
非 的逻辑表达式:

在计算机中常用第二种表达方式
两种表达方式,读成 X等于A非
also can read as:
“X equals NOT A”
“X equals the inverse of A”
“X equals the complement of A”
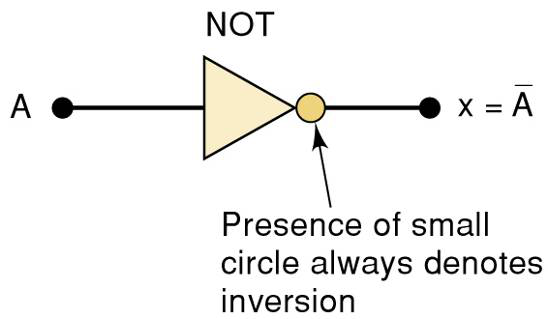
非 的符号:
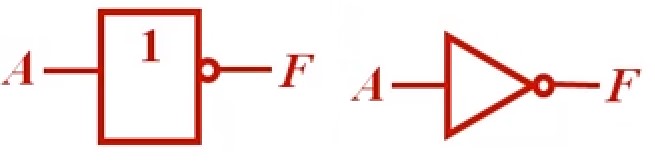
左边是矩形轮廓符号(国标符号),右边是特定外形符号(国外流行符号)
非 的真值表
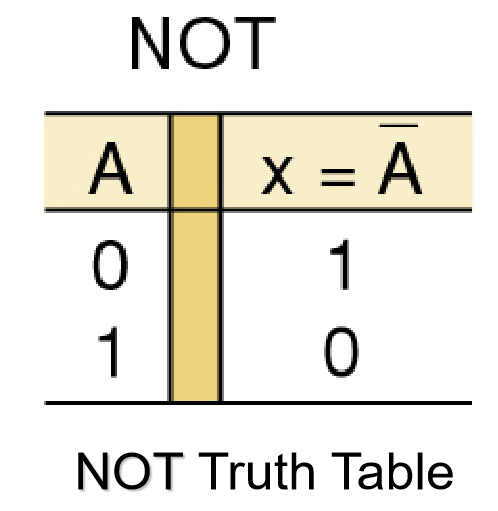
此电路始终只有一个输入,并且输出的终与此输入的相反
非电路通常被称作逆变器(INVERTER)
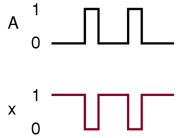
逆变器(INVERTER)对波形上所有点的输入信号进行反相(补码)
OR、AND和NOT的规则汇总
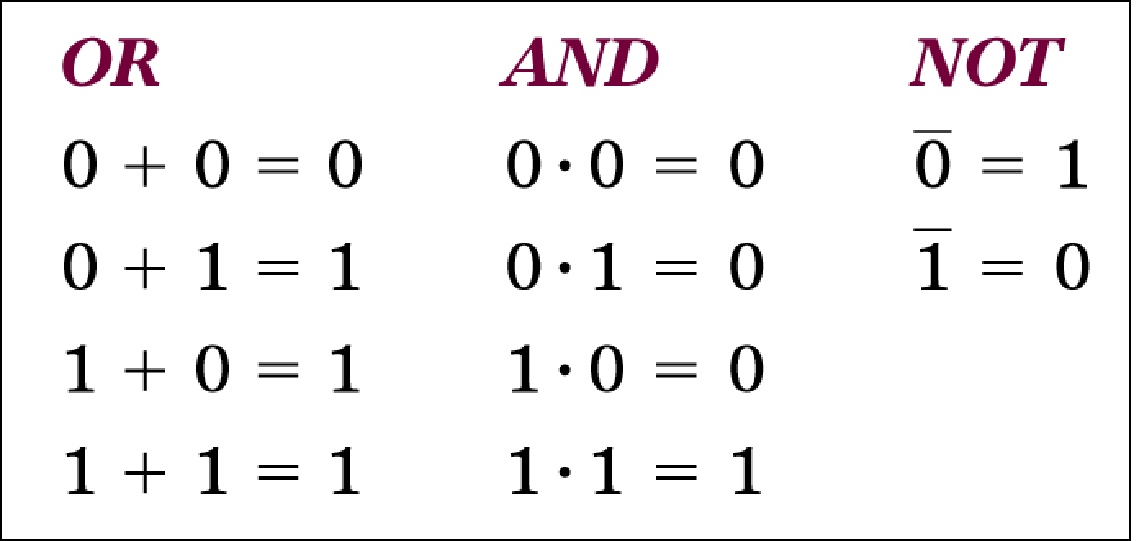
运算法则
如果表达式同时包含AND和OR门,则首先执行AND操作
也就是先算A·B
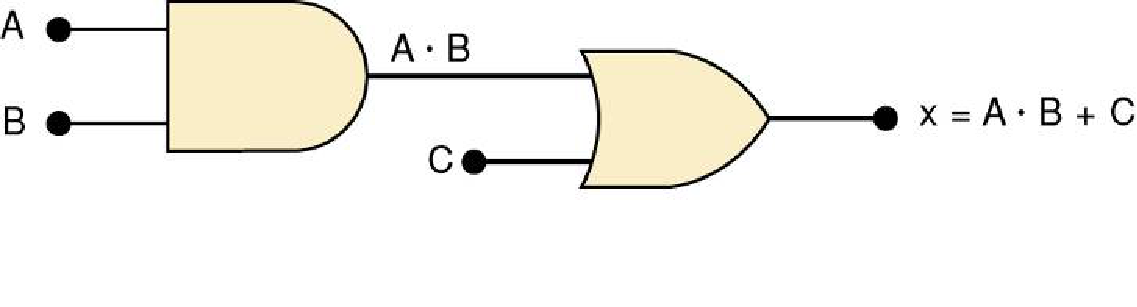
除非表达式中有括号,此时先算括号里面的
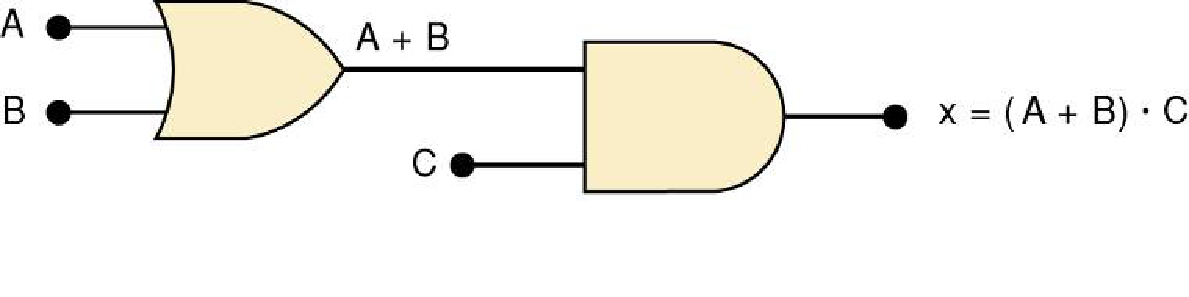
只要有逆变器(INVERTER)存在,输出等于输入上面加一横线
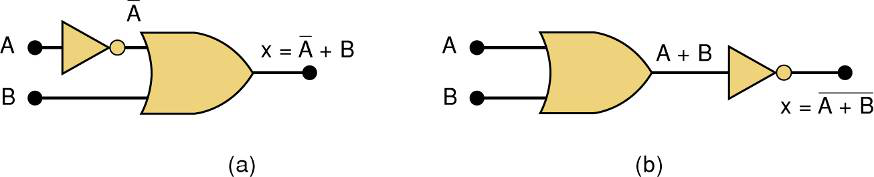
再来看复杂点的例子
(1)
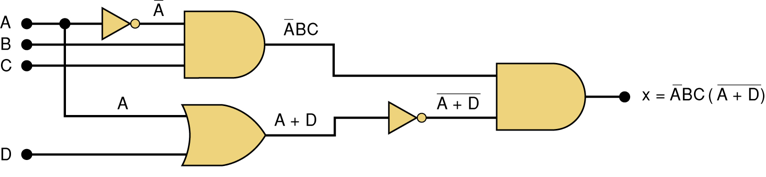
(2)
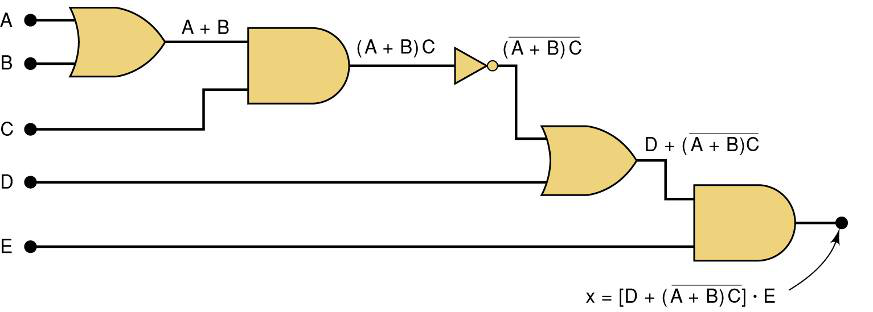
写成表达式的计算:
首先将值代入进去
然后计算 非(NOT)的
括号优先
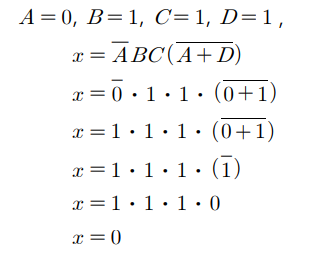
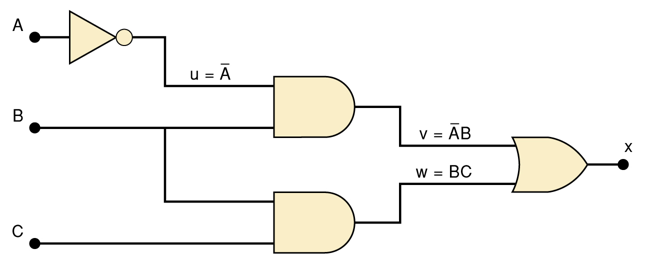
利用真值表解决问题
分析由多个逻辑门组成的电路的最佳方法是使用真值表
它允许您一次分析一个门或逻辑组合。
它使您可以轻松地重新检查您的工作。
完成后,您将获得一张对逻辑电路表,对故障排除 有巨大好处。
如图所示
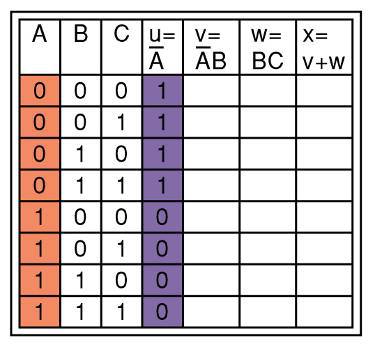
首先用真值表列出所有组合
这包括了输入的A B C ,还有这些输入对应组合起来的列
节点u是将A进行非运算
然后再来求节点V,当节点u和B同时成立的时候,就成立,记为1
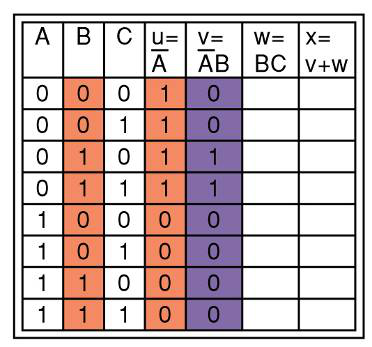
节点W,将B和C进行 与运算
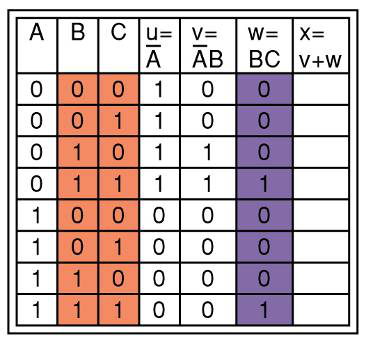
节点X,将V和W进行 或运算
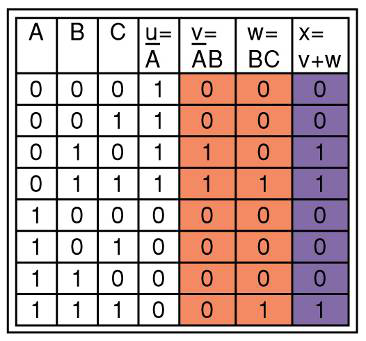
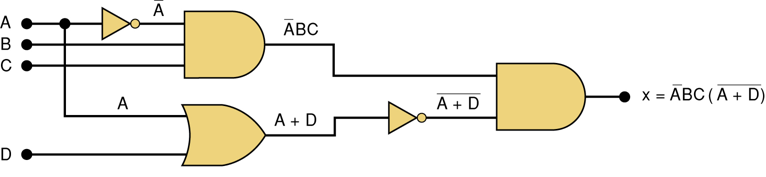
真值表
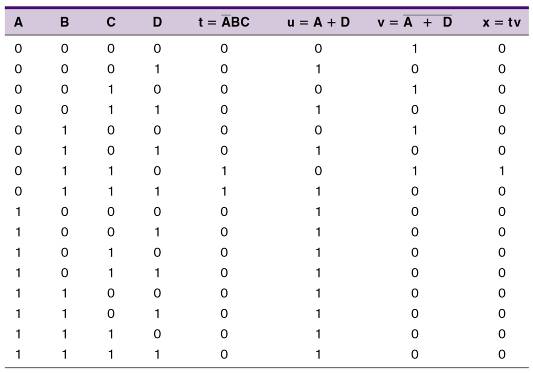
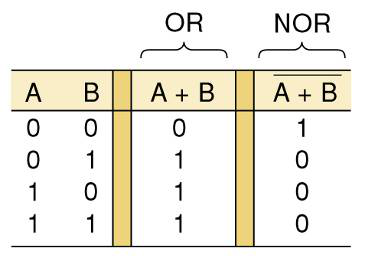
NOR 或非门
只有当两个输入A和B为低电平(逻辑0)时输出为高电平(逻辑1)。也可以理解为任意输入为高电平(逻辑1),输出为低电平(逻辑0)。
或非门 的逻辑表达式
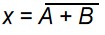
或非门 的符号
下面这张图说明了或非门的符号是如何演变而来的
(图片上方是 或非门的符号,图片下方是表示或非门拆开来看本质是 或门加非门的一个组合)
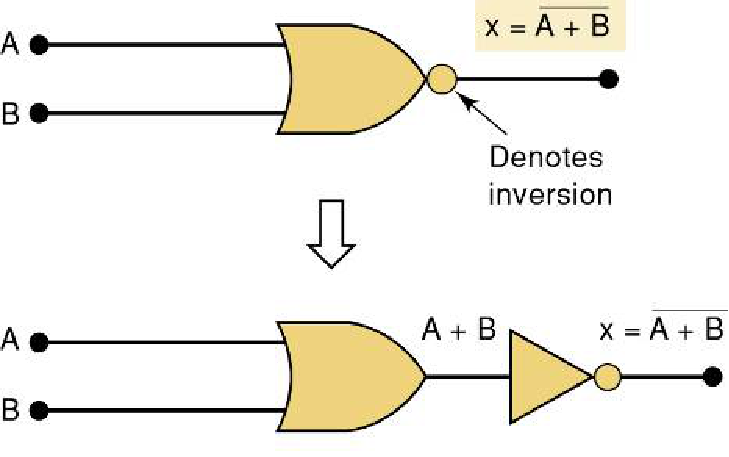
相当于是或门OR + 非门NOT 的一个组合 :NOR
左边是一个 或门,右边小圆点是非门
或非门 的真值表
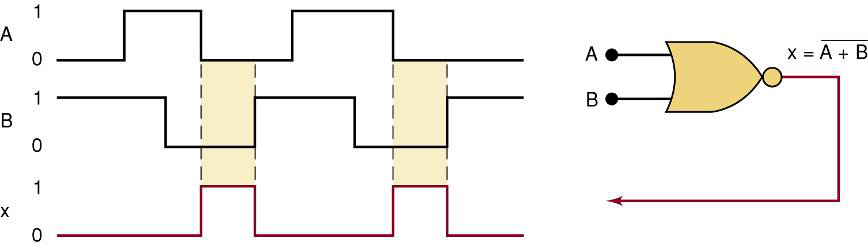
波形图
NAND 与非门
若当输入均为高电平(1),则输出为低电平(0);若输入中至少有一个为低电平(0),则输出为高电平(1)。与非门可以看作是与门和非门的叠加。
与非门 的逻辑表达式
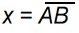
与非门 的符号
下面这张图说明了与非门的符号是如何演变而来的
(图片上方是 与非门的符号,图片下方是表示与非门拆开来看本质是 与门加非门的一个组合)
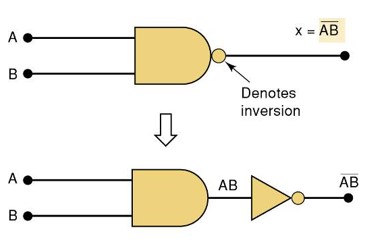
相当于是与门AND + 非门NOT 的一个组合 :NAND
左边是一个 与门,右边小圆点是非门
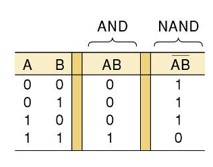
与非门 的真值表
波形图
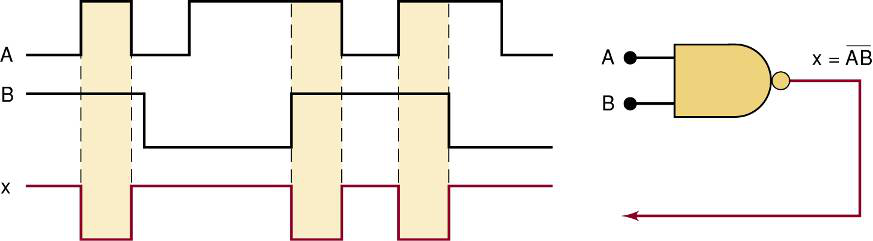
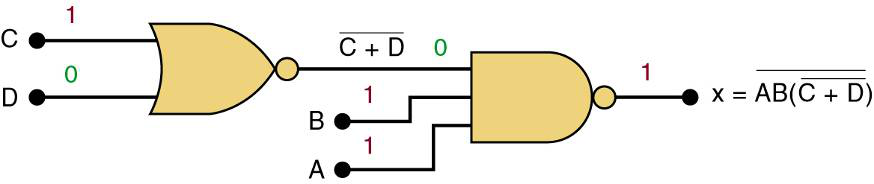
这是一个NOR和NAND组合的例子
这篇文章将会介绍布尔定理:
http://www.yuofyou.cn/20200920/1380.html