BCD码
用4位二进制数来表示1位十进制数中的0~9这10个数码
说白了就是前面提到的 十进制转二进制
BCD码里面又有8421码,2421码,5421码,说白了,就是数轴上面的数字不一样
对应位就不一样
举个例子十进制数8
在8421码里面是1000
在2421码里面是1110,因为2+4+2+0=8
在5421码里面是1011,因为5+0+2+1=8
请注意!!!是用4位二进制数来表示1位十进制数
这意味着,假设十进制数74 它的BCD码应该是
7:0111
4:0100
74:01110100
格雷码
在一组数的编码中,若任意两个相邻的代码只有一位二进制数不同,则称这种编码为格雷码(Gray Code),另外由于最大数与最小数之间也仅一位数不同,即“首尾相连”,因此又称循环码或反射码。
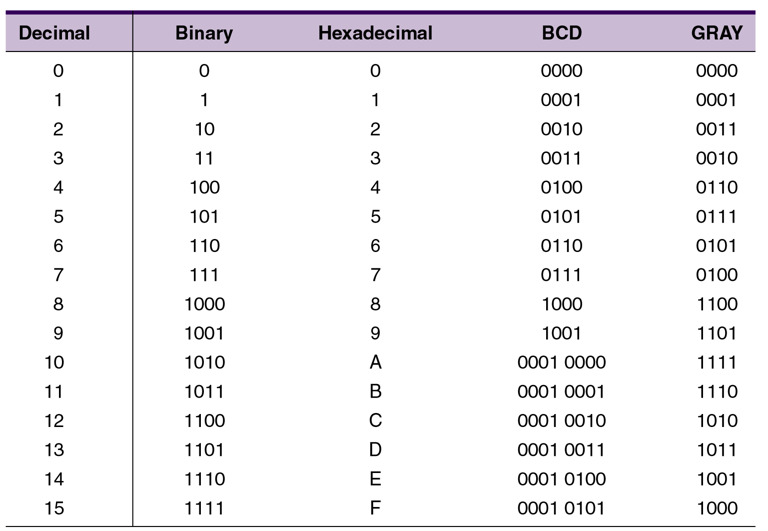
| 十进制数 | 格雷码 |
|---|---|
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0011 |
| 3 | 0010 |
| 4 | 0110 |
| 5 | 0111 |
| 6 | 0101 |
| 7 | 0100 |
| 8 | 1100 |
| 9 | 1101 |
| 10 | 1111 |
| 11 | 1110 |
| 12 | 1010 |
| 13 | 1011 |
| 14 | 1001 |
| 15 | 1000 |
产生的规律:(以下说的改变就是把0改成1,或者把1改成0)
第一步:改变最右边的那个数值
第二步:改变右起第一个为1的数左边的值
一直重复
奇偶校验码
信息在存储和传输过程中很容易出现错误,需要进行检错。这个时候需要用到奇偶校验码。
奇偶校验码就是在原本这个数中再加入1位数
奇校验
需要保证加了校验码以后所含的1的个数为奇数。
偶校验
需要保证加了校验码以后所含的1的个数为偶数。
举个例子
现有一个数1100111,采用偶校验
这个数现在一共是五个一,偶校验需要把它变成偶数个一,所以在后面添1
再举个例子
现有一个数00000100,采用奇校验
但是现在只有一个1,已经是奇数了,所以只需要在后面添0
弊端
奇偶校验只能检错不能纠错
如果出现两位错,奇偶不变的情况,就无法判断出错
注意
The parity bit may be added at either end of a group.
需要注意的是:这个校验位可以在任意一端写,就是说可以写在这组数的前面,也可以写在最后面。