卡诺图是一种图解工具，用来化简逻辑方程式或者把一个真值表以简单而有规律的方法转换为相应的逻辑电路。卡诺图也称K图(K map)
尽管卡诺图可用来解决涉及到任意输入变量的问题，但实际上限制5个或6个输入变量以内
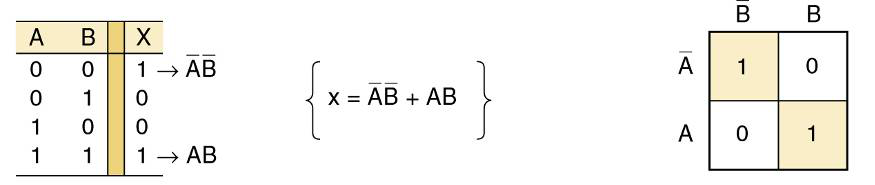
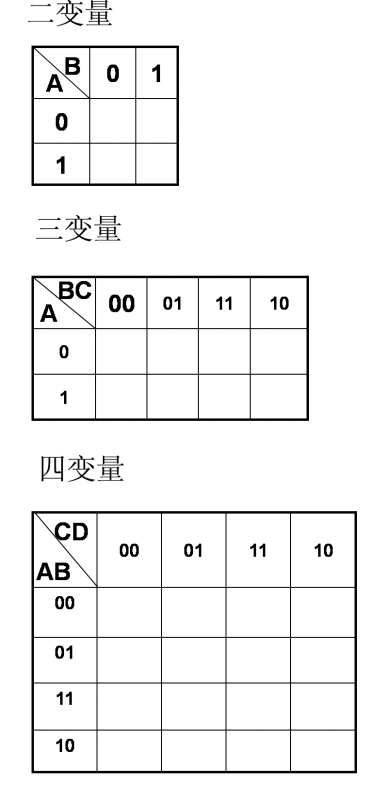
将真值表值放在K图中 这里显示的是一个双输入变量的图
卡诺图的格式
下面分别给出2输入、3输入、4输入变量卡诺图的三个例子和相应的真值表
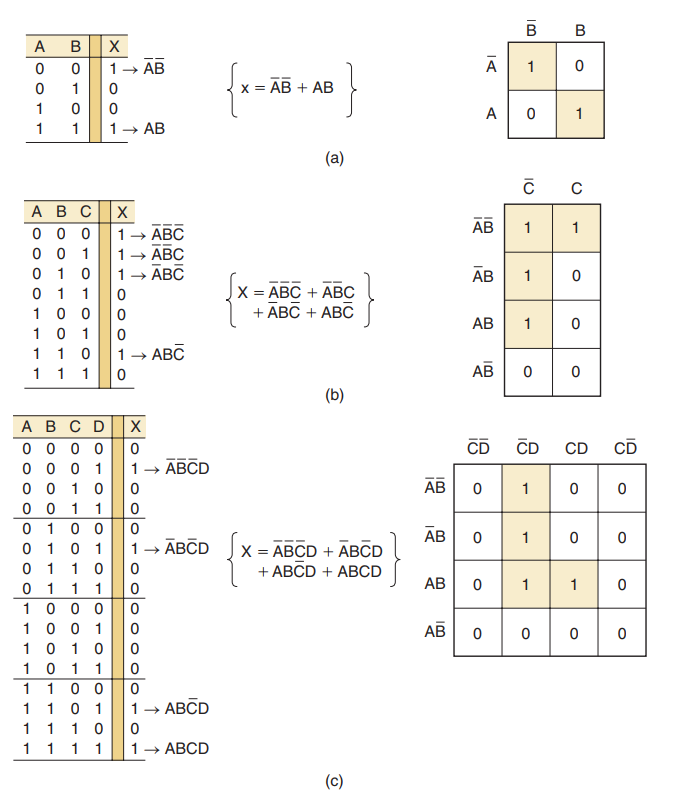
真值表中的每一种输入组合与卡诺图中的一个小方格相对应
例如在(a)中，真值表A=0,B=0的情况对应于卡诺图中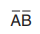
小方格。由于真值表对于这种情况输出x=1，所以在卡诺图内也放置1
标记卡诺图使水平相邻的小方格仅有一个变量不同。例如，在4变量卡诺图中，左上角的小方格是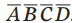
，其右边相邻的小方格是
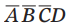（仅变量D不同），类似的垂直相邻的小方格也仅有一个变量不同
为了使水平和垂直相邻的小方格仅有一个变量不同，从上到下标记的顺序必须是：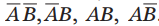
，同样从左到右的顺序必须是：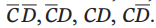
一旦卡诺图填写了0和1，就可以把这些含1的小方格或在一起从而得到输出x的与或表达式，在如图(b)所示3变量卡诺图中，小方格中有4个含1，因此就可以得出输出x的与或表达式
注意：变量必须按照以下的顺序进行书写
画包卡诺图
在卡诺图中将含1的小方格适当组合可简化输出x的表达式，组合这些1的过程叫做画包卡诺图
2个一组画包围圈
如图所示是一个特定的3变量真值表的卡诺图，这个卡诺图包含两个1，且它们垂直相邻
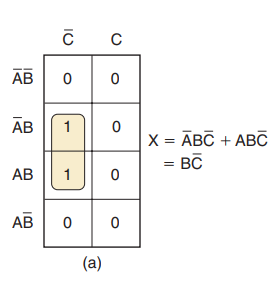
第一个表示：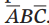
第二个表示：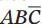
观察这两项，发现只有A以原变量和反变量的形式出现，而B和C保持不变。这两项圈起来的组合可以消去变量A，因为变量A以原变量和反变量的形式出现两次，证明如下：
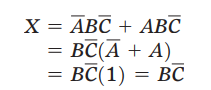
同样的原理也可以适用于任何一对垂直或水平相邻的1，图（b）所示是两个1水平相邻的例子
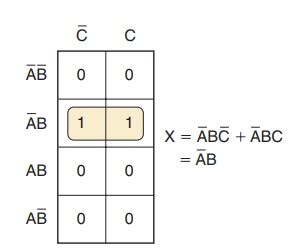
对着两项可包围消去变量C，因为C以原变量和反变量的形式出现两次，得到的结果为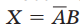
另外一个例子如下图所示，在卡诺图中，最上面的一行和最下面的一行中的小方格是相邻的
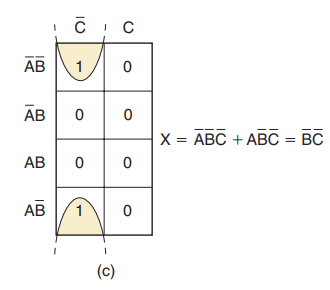
因此此卡诺图中两个1可圈起来形成
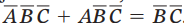的结果
下图所示的卡诺图中有两个1可圈起来。
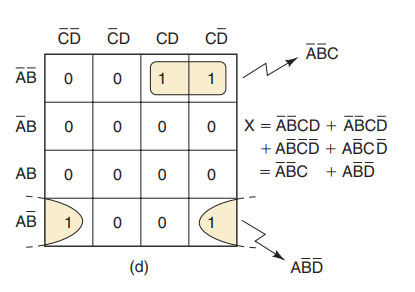
顶行的两个1水平相邻，底行的两个1也相邻，因为卡诺图中最左边一列和最右边一列的小方格是相邻的。
当顶行的两个1圈起来时，变量D被消除。
对底行的一对1花圈，消去变量C。这两项相或给出x的最后结果为：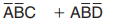
4个一组画包围圈
卡诺图可能包含一组4个彼此相邻的1。4个彼此相邻的1叫做四重组。如图所示
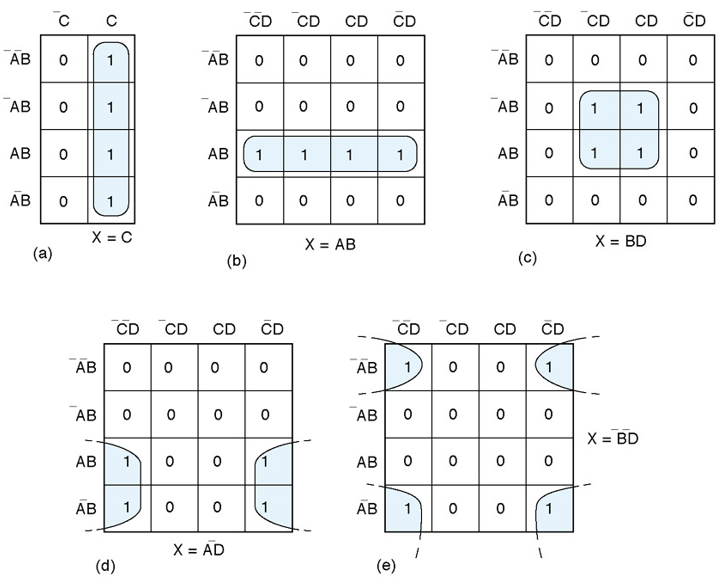
（a）中4个1垂直相邻
（b）中4个1水平相邻
（c）中卡诺图所包含的4个1彼此相邻，形成正方形
（d）和（e）中，4个1也是分别相邻的，因为前面也说过，卡诺图中顶行和底行看做是彼此相邻的，同样，最左边一列和最右边一列看做的相邻的
当对一个司重组画包围圈后，所合成的项仅当包含四重组中在所有小方格不改变形式的变量。
例如在（a）中，包含1的四个小方格，发现其中只有C保持不变（a和b均以原变量和反变量的形式出现）。因此化简后x的表达式为x=C。证明如下：
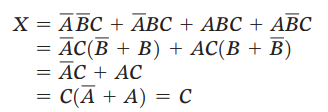
另外一个例子，（d）中，包含1的4个小方格是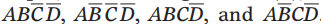
，观察这些项发现只有A和D'保持不变。因此化简后x的表达式是：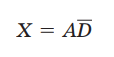
8个一组画包围圈
一组里面有8个1彼此相邻叫做八重组；在4变量卡诺图中，当对八重组画包围圈时，将消去3个变量，因为仅有一个变量保持不变
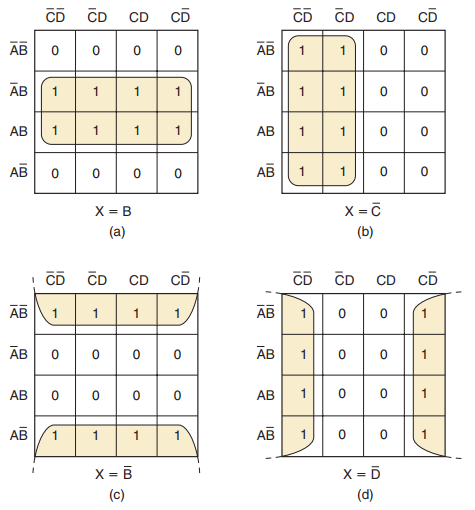
如图所示（a）中被圈起来的8个小方格，可见仅变量B在8个小方格中保持同一形式；其他变量以原变量和反变量的形式出现
对于这个卡诺图，x=B
完整的简化过程
对于任意大小的包围圈，可归纳其规律如下：
当变量以原变量和反变量的形式出现在一个包围圈内时，这个变量可从表达式中消去。对于包围圈内所有小方格保持不变的那些变量，必然出现在最后的表达式中
包含1的包围圈越大，消去的变量越多。确切地说，
两个小方格形成的包围圈消去一个变量
四个小方格形成的包围圈消去两个变量
八个小方格形成的包围圈消去三个变量
应用卡诺图法化简布尔表达式时，可按下述步骤进行：
第1步：画卡诺图并求所给逻辑函数的卡诺图表示，即在和真值表中1相应的小方格中置1，其它小方格置0
第2步：观察卡诺图中1的相邻情况，圈出那些与其它任何1不相邻的含1的小方格
第3步：寻找仅有两个1相邻的情况，圈出每一对仅有两个1相邻的小方格
第4步：圈出任一八重组，即使它包含的某些1已被别的圈包围
第5步：圈出任一四重组，它可以包含一个或多个已经被别的圈包围的1，确保所用的圈的个数最少
第6步：圈出任何一对需要包含但没有被别的圈包含的1，确保所用圈的个数最少
第7步：把每个圈所形成的的与项相或
例题1
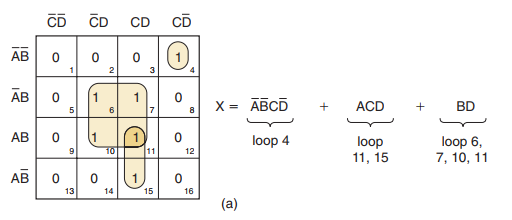
假设第一步已经由此问题的真值表得到
第2步：小方格4（小方格右下角的数字编号）含1但与其它任一个互不相邻，把它单独圈出并记为loop4
第3步：小方格11仅与小方格15相邻，圈出这一对并记为loop11，loop15
第4步：此图中没有8个含1小方格相邻
第5步：小方格6、7、10和11形成四重组，圈出这个四重组并记为loop6，loop7，loop10，loop11，注意小方格11被重复利用，尽管它已是loop11，loop15的一部分
第6步：所有的1已被圈入
第7步：在x的表达式中，每个包围圈产生一项，loop4是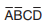
，loop11，loop15简化为ACD（消去变量B），loop6，loop7，loop10，loop11简化为BD（消去A和C）
例题2
假设第一步已经完成
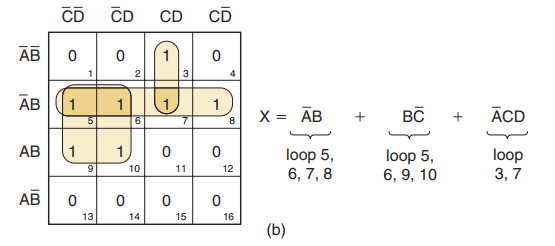
第二步：此图中没有孤立的1
第三步：小方格3中的1仅与小方格7中的1相邻，圈出这一对1（loop3，loop7）产生于A非CD项
第四步：此图中没有八重组
第五步：图中有两个四重组，小方格5、6、7和8形成一个四重组，圈出这个四重组产生与项A非B，另一个四重组由小方格5、6、9和10组成，圈出这个四重组因为它含有两个前面没有圈入的小方格，所产生的与项为BC非
第六步：所有的1已圈入
第七步：由3个包围圈所产生的的与项相或，得到x的表达式
例题3
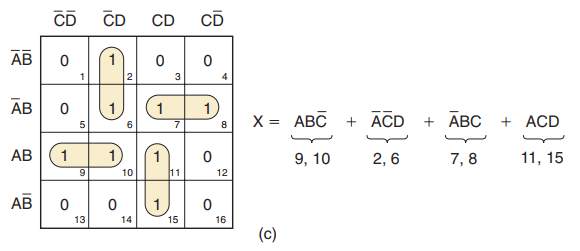
第二步：此图中没有孤立的1
第三步：小方格1中的1仅和小方格6中的1相邻，圈出这一对1，类似地，小方格9仅与小方格10相邻，圈出这一对与项；同样，loop7，loop8和loop11，loop15分别产生与项
第四步：此图中没有八重组
第五步：图中小方格6、7、10、11形成四重组，然而它不必圈出，因为其中的所有1已包含在其它的圈内
第六步：所有的1已圈入
第七步：由4个圈产生的与项相或，得到x的表达式
例题4
图（a）所示的卡诺图
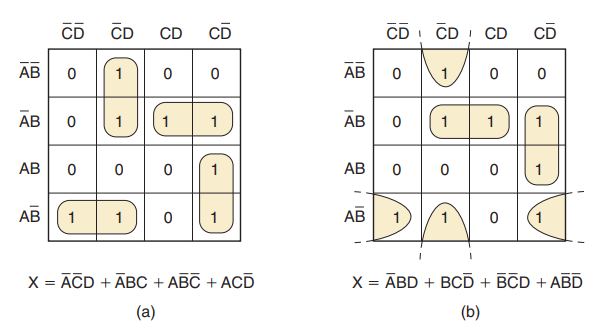
第二步：图中没有孤立的1
第三步：图中没有1仅与其它的1个1相邻
第四步：图中没有八重组
第五步：图中没有四重组
第六步和第七步：图中出现多个1相邻的情况，必须用最少数量的包围圈圈入所有1.对于此卡诺图有两种可能的圈法，每种仅需4个包围圈。图b是另外一种解法。两种是一样的
由输出表达式填写卡诺图
当所要求的输出是由布尔表达式而不是真值表给出时，可采用下述步骤来填写卡诺图：
- 如果所给表达式不是与或表达式，把它转换为与或表达式
- 对与或表达式中的每一个乘积项，在卡诺图中相应的小方格里填1，此小方格标记包含相同的输入变量组合，在所有其他小方格里填0
例题：
用卡诺图简化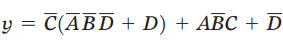
- 用逻辑乘展开第一项得：
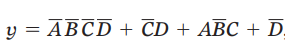，此式为与或表达式 - 对于第一项，在卡诺图里的小方格A非B非C非D非里填1
对于第二项，在标记C非D的所有小方格里填1,
对于第三项，在标记AB非C的所有小方格里填1
对于第四项，在标记D非的所有小方格里填1，也就是说，最左边和最右边全是1
得到如图所示的卡诺图
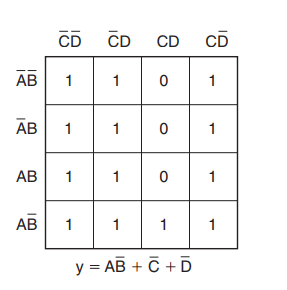
最后画圈化简
“无关项”状态
对于所设计的有些逻辑电路，存在某些输入条件使其输出没有确定的电平，通常是因为这些输入条件永远不会出现。换句话说，有一些输入电平组合，可以不管其输出是高电平还是低电平。下图就是一个例子：
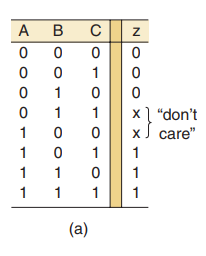
对于输入条件ABC=100和ABC=011，输出z是0还是1不确定，对于这些输入条件，输出以X来表示，X表示无关状态。无关项状态的形成有多种原因，最常见的是在有些情况下，某些输入组合永远不会出现，因此，对这些条件没有确定的输出。
对于任一无关项目状态，电路的设计者可自由选择输出是0还是1，以便形成最简输出表达式。例如，上面的真值表所对应的卡诺图如下图所示
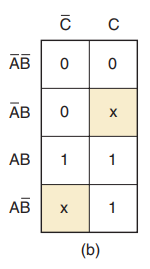
在无关项处打X。此处，设计者希望AB非C非小方格内的X变为1，在A非BC小方格内变X为0，因为这样可产生一个司重组，画包围圈合并后形成Z=A ，如下图所示
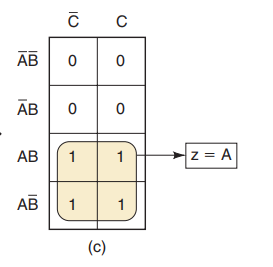
每当无关项出现时，我们必须决定哪个X变为0，哪个X变为1，已形成最优的卡诺图包围圈（即最简表达式），这个决定经常是不容易做出的。
例题：设计一个三层楼房的电梯门控制逻辑电路。图（a）所示电路有4个输入，M是一个逻辑信号，当电梯运动时M=1，停止时M=0。F1、F2、F3是楼层指示器的信号，它们通常情况下是低电平，仅当电梯定位在特定楼层平面时，它变为高电平。例如，当电梯与二层地面平齐时，F2=1,F1=F3=0。电路输出是OPEN信号，它通常是低电平，当电梯门打开时它变为高电平
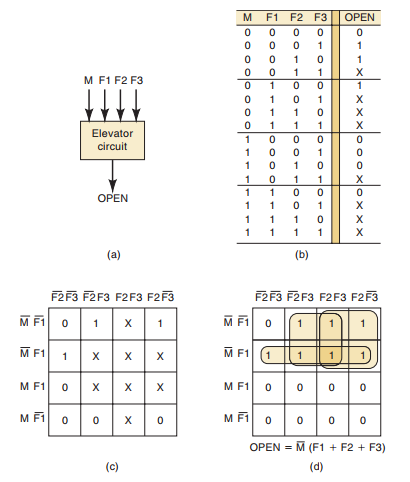
对输出信号OPEN，可按下述方法对其列出真值表，如图（b）所示
- 由于电梯在某一时刻不可能同时与两个或三个楼层对齐，因此，在任一给定时间，仅有一个楼层的输入信号可能是高电平。这意味着在真值表中，多于一个楼层输入是1的这些情况是无关项，对于一个以上F输入1的8种情况，输出OPEN一栏可填写X
- 查看其他8种情况，当M=1时，电梯在运动中，OPEN必须是0，因此此时不希望打开电梯门，当M=0时（电梯停止），我们希望OPEN=1，规定一个楼层输入是1.当M=0且全部楼层输入是0时，电梯虽然停止但没有与任一层对齐，因此我们希望OPEN=0，以便使门保持关闭
现在真值表已完成，可把真值表的信息转换为卡诺图，如图(c)所示。此卡诺图仅有3个1，但它有8个无关项，通过把这些无关项小方格中的4个变为1，能形成包含原来1的四重组，如图（d）所示，这就是所能得到的最简输出表达式。验证所画出的包围圈形成的OPEN输出表达式为