在数字系统中频繁出现的两个特殊逻辑电路是异或电路和同或电路
异或
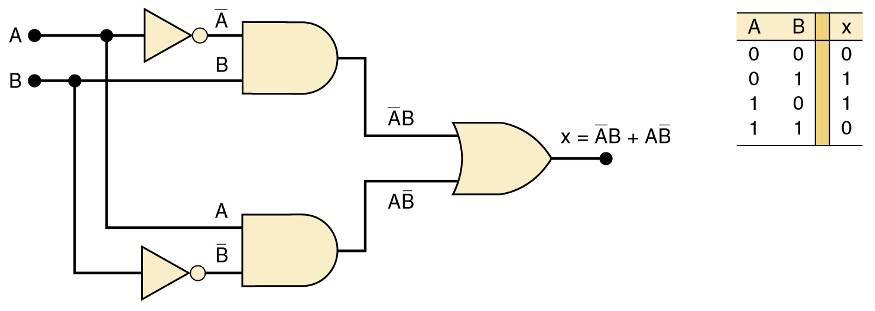
如图所示的逻辑电路，可见其输出表达式是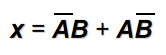
其对应的真值表表明：x=1的两种情况是A=0,B=1（第一项）和A=1，B=0(第二项)，换句话说：每当两个输入电平相反时，电路输出高电平
这就是异或电路，简称XOR
事实上，异或电路有它自己的符号，如图所示
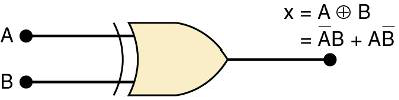
假设这个符号包含异或电路所具有的逻辑功能，因此，它与异或电路有同样的表达式和真值表。
异或电路通常叫做异或门，认为它是又一种逻辑门类型。
一个异或门仅有两个输入端，没有3输入或者4输入的异或门。
对于2输入组合有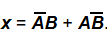
有时也采用简写形式来表示异或输出表达式：
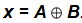
此处符号
表示异或运算。
其表明：
仅当一个输入是高电平时，其输出将是有效高电平
异或门的特点归纳如下：
1.它仅有两个输入端，其输出为：
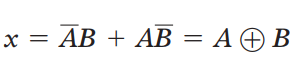
2.仅当两个输入电平不同时，其输出是高电平
有几个可买到的集成电路芯片内含异或门。下面所列是四异或门，即每个芯片含4个异或门
- 74LS86 四异或门 (TTL 系列)
- 74C86 四异或门 (CMOS 系列)
- 74HC86 四异或门 (高速 CMOS)
同或（异或非）
同或电路（简称XNOR）的工作原理与异或电路完全相反。下图是同或电路及其真值表。
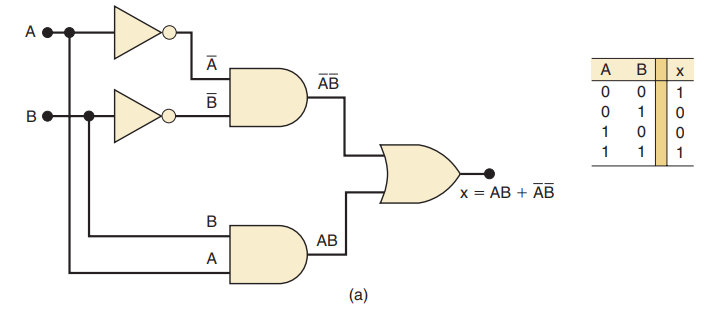
其输出表达式为：
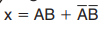
此式及真值表均表明，x为1的两种情况是：A=B=1(AB项)和A=B=0(A非B非项)，换句话说：每当两个输入电平相同时，同或门输出高电平
同或电路的输出恰好是异或电路输出的反相。同或门的传统符号是在异或门符号输出端加小圆圈。如图所示
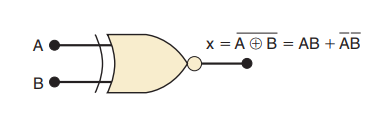
其表明：
仅当一个输入是高电平时，其输出变为低电平
同或门也仅有两个输入端，它们组合形成的输出是：
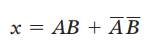
同或门输出表达式的简写形式是：
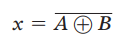
此式是异或运算的反相，有关同或门的特点归纳如下：
- 它仅有两个输入端，其输出是：
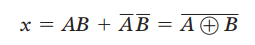
- 仅当两个输入电平相同时，其输出是高电平
有几个可买到的集成电路内含同或门，下面所列的是四同或门，即每个芯片上含4个同或门
74LS266 四同或门 (TTL 系列)
74C266 四同或门 (CMOS 系列)
74HC266 四同或门 (高速 CMOS)
例1
电路和输入波形如图所示，试确定其输出波形
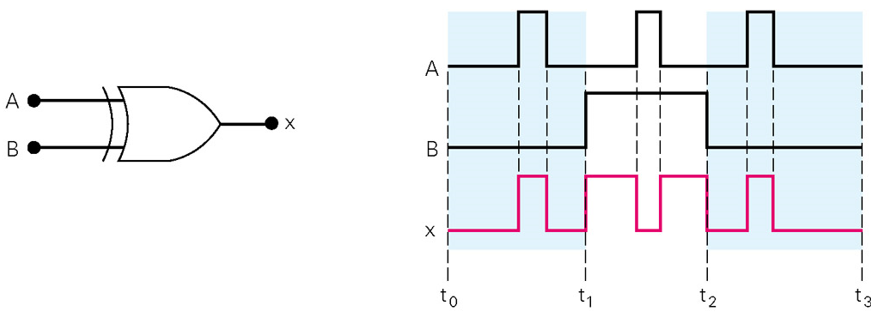
首先回顾一下：仅当输入处于不同电平时，异或门输出变为高电平。可以确定它的输出波形
观察输出x的波形 可以发现以下几个问题
- 在B=0的时间范围内，x的波形与输入A的波形一样，它发生在时间间隔t0~t1和t2~t3之间
- 在B=1的时间范围内，x的波形是输入A波形的反相，它发生在时间间隔t1~t2之间
- 上述分析明显表明，异或门可以作为可控反相器；即一个输入端可用来控制另一个输入端的信号是否被反相
例2
x1x0表示两位二进制数，它可取其任一值（00,01,10,11）；例如当x1=1和x0=0时，二进制数是10，以此类推，类似的，y1y0表示另一个两位二进制数。设计一个逻辑电路，用x1、x0、y1和y0作为输入，仅当两位二进制数x1x0和y1y0相等时，输出变为高电平
首先对于16种输入状态列真值表
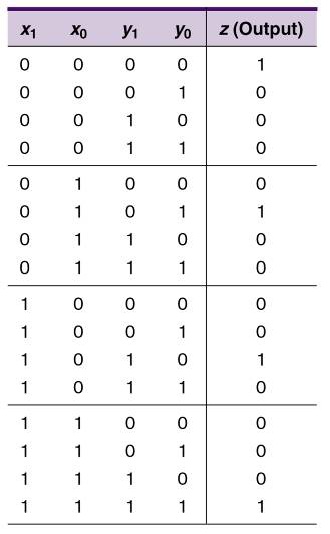
每当x1x0的值和y1y0的值一样时，输出z是高电平，也即x1=y1，且x0=y0 真值表表明有4种这类情况，现在可以继续按常规过程去做：求取z的与或表达式、做必要的化简、电路实现。然而，这个问题的特点使它很适合用同或门来实现，稍加思索即可用较少的工作量而形成简单的解决方案。由下图可见
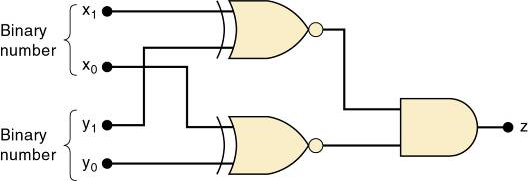在这个逻辑电路图中，x1和y1作为一个同或门的输入，x0和y0作为另一个同或门的输入，仅当其输入相等时，每一个同或门的输出才是高电平。即当x0=y0，且x1=y1时，两个同或门输出均是高电平