功能分类

渐近增长率、渐进阶、或函数阶数

对忽略常数因素和小输入的函数进行比较和分类

big oh O(g)， big theta Θ(g)，big omega Ω(g)

Ω(g): 增长速度至少与g一样快的函数
Θ(g): 增长速度与g相同的函数
O(g): 增长速度不超过g的函数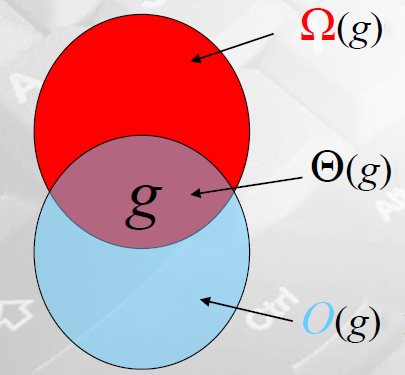

T（n）

int fun1(void)
{
    printf("hi");
    return 0;
}

上面这条语句函数内部总共执行了2次（2条语句），T(n)= 2

int fun2(void)
{
    for(int i=0; i<n;++i){
        printf("hi");
    }    
return 0;
}

上面这条语句函数内部总共执行了3n+3次，T(n)= 3n + 3

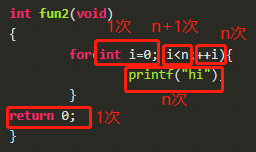
T(n)表示当输入为n时，某段代码的总执行次数
n表示输入数据的大小或者数量

但是当代码量比较多的时候 使用T(n)就会比较麻烦了，所以算法一般使用T(n)的简化估算值，这个简化的估算值叫 时间复杂度

大o表示法 O(g)

T(n)= 常数 时，可以直接估算成 1
因此，上面第一个例子中T(n) = 2 的时间复杂度就是O(1)

T(n)= 常数 × n + 常数 时，直接省略掉第二个常数，第一个常数可以直接估算为1 所以它的时间复杂度就是n
因此，上面第二个例子中T(n)= 3n + 3的时间复杂度就是O(n)

另外一种情况，
T(n) = 5n³ + 6666n² +233
在这个多项式里，可以直接省略低次项和常数，只看最高次项，省略掉最高次项的系数 ，它的时间复杂度就为O( n³)

总结：
T(n)是不是常数

• 是：时间复杂度为O(1)
• 不是：时间复杂度为O(保留T(n)的最高次项并且去掉最高次项的系数)