我们分析算法的目的是为了改进它们。
如果可能的话,对于一个问题我们需要在多个可用的算法中选择。
- 正确性
- 所做工作的数量和使用的空间
- 最优性、简单性
正确性 可以被证明!
一个算法由将输入(前提条件)转换为输出(后置条件)的步骤序列(操作、指令、语句)组成
证明
如果先决条件得到满足
那么后置条件将为真
当算法终止时
完成的工作数量
我们希望有一个衡量工作的标准,告诉我们关于方法效率的东西
独立于计算机、编程语言、程序员和其他执行细节
通常取决于输入的大小
最坏情况下的复杂度
Dn是所考虑的问题的大小为n的输入集合,让I是Dn的一个元素。
t(I)是算法对输入I进行的基本操作的数量。
用W(n) = max{t(I) | I ∈ Dn}称为算法的最坏情况下的复杂性
W(n)是算法对任何大小为n的输入进行的最大基本操作数。
平均情况分析
算法可能在某些输入上比在另一些输入上运行得更快。在这种情况下,算法的运行时间空余表示为算法在所有可能输入上运行时间的平均值。
在平均情况分析中,我们计算所有可能的输入的运行时间,把所有的时间加起来除以数量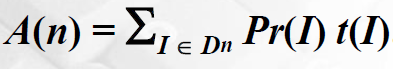
空间使用和简单化
空间的使用
- 如果使用的空间量取决于特定的输入,可以做最坏情况和平均情况的分析。
- 时间和空间之间的权衡
算法的简单性是一种美德
最优性
每个问题都有其固有的复杂性
- 有一些方案解决这个问题所需的工作量最小
为了分析一个问题的复杂性。
- 我们选择一类算法(通常是通过指定算法允许执行的操作类型)和一个衡量复杂性的标准,例如,要计算的基本操作。
- 然后,我们可以问,解决这个问题实际上需要多少操作。
如何证明一个算法是最优的
设计一个有效的算法,称之为A。分析A并找出最坏情况下的复杂度W(n),(n为输入的大小)
对于某个函数F,证明一个定理,说明对于所考虑的同一类中的任何算法,都有一些大小为n的输入,对于这些输入,该算法 必须至少执行F(n)步。
如果WA(n)=F(n)
- 则算法A是最优的(对于最坏的情况)。
否则可能有更好的算法
或者可能有更好的下限。
例
在一个(未排序的)数组中找到最大的 n
int findMax(int[] E, int n)
int max;
max = E[0]; // Assume the first is max.
for (index = 1; index < n; index++)
if (max < E[index])
max = E[index];
return max;找到W(n)
一个数组成员与另一个数组成员的比较 或一个存储变量进行比较。
- 最坏情况分析
对于任何大小为n的输入,正好有n-1个基本的操作
WA(n) = n-1
找到F(n)
- 假设数组中的成员都是不同的
(允许用于寻找最坏情况下的下限) - 在一个有n个不同成员的数组中,n-1个成员不是最大值。
- 要得出一个成员不是最大值的结论,它必须至少比其他一个成员小。而且,为此需要进行一次比较(基本操作)
- 所以至少要进行n-1次基本操作。
- F(n) = n - 1
W(n)=F(n)算法A是最优的