与或表达式
逻辑电路简化和设计方法，要求逻辑表达式是与或形式(SOP)。
这种形式的例子如：
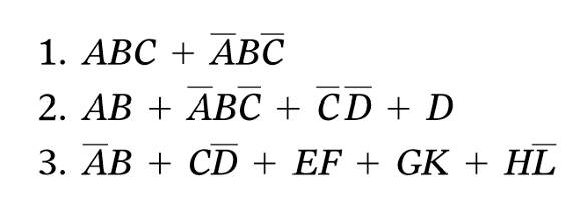
每一个与或表达式由两个或多个与项(乘积)相或组成，每个与项由一个或者多个变量组成，各个变量以原变量或者反变量的形式出现。
注意：在与或表达式中，一个非号不能覆盖多个变量
或与表达式
有时还用到另外一种逻辑表达式，即或与表达式(POS)，它由两个或者多个或项（和）相与组成。每个项包含一个或者多个变量，各变量以原变量或反变量的形式出现，下面是例子：
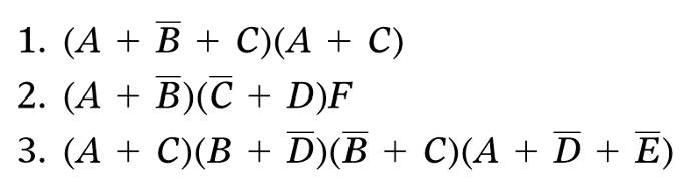
化简逻辑电路
当得到一个逻辑电路的表达式的时候，就可能可以化简为包含较少项或者较少变量的逻辑功能
这样化简以后，比原电路体积小且更经济，电路的可靠性得到了改善，减少了可能的潜在电路故障
如下图
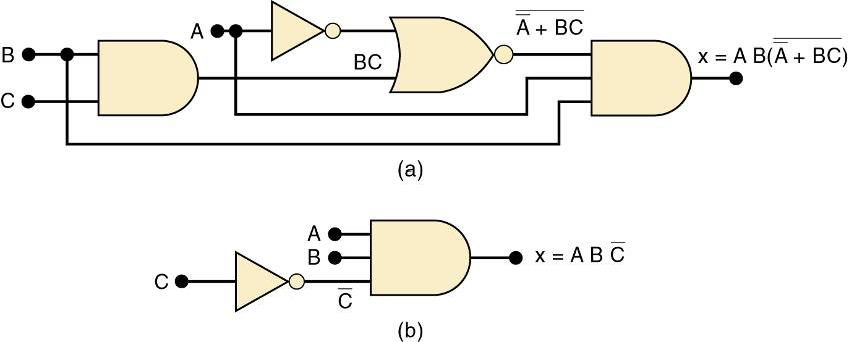
(a)可以简化为(b)
代数化简法
前面的文章说明了布尔代数定理，可以用它来化简逻辑电路的表达式。但是，往往应该使用哪个定理是不明显的，且没有一种容易的方法来辨别化简后的表达式是不是最简的，因此随着经验的增加，应该掌握获得合理结果的方法
下面的例子说明布尔定理用于化简逻辑表达式的许多方法，基本包含两个步骤：
- 反复应用摩根定律和分配率，把原表达式变换成与或表达式
- 在原表达式变成与或表达式的情况下，检查乘积项（与项）的公共因子，如果可能的话提取公共因子，看能不能消去一项或多项
例1
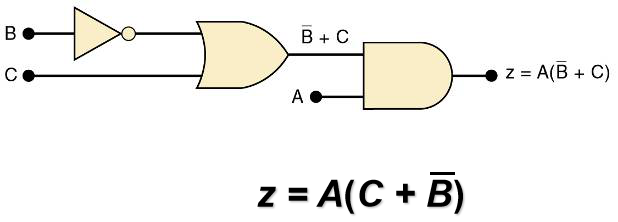
简化如图所示的逻辑电路
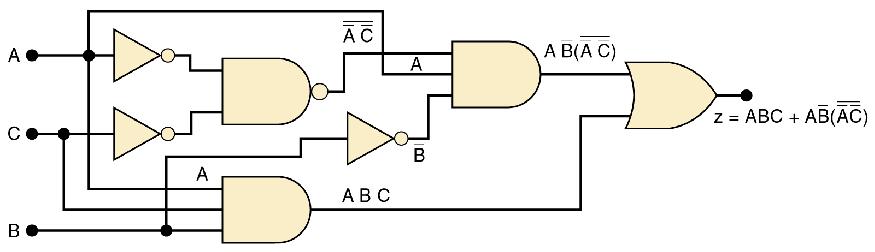
第一步先求出这个电路的输出表达式，结果为：
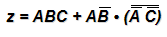
利用摩根定理分拆所有大的非号并应用分配率消去括号
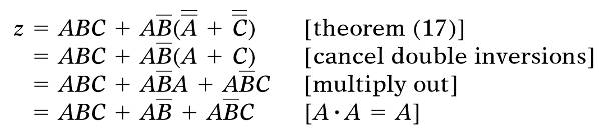
复习一下这些定理
第一步的定理17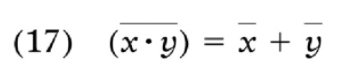
第二步由于A和C上面是两个非号可以直接删去
第三步去括号(直接乘进去)
第四步观察第二项有个A·A 所以使用A·A=A直接消去一个A
因为有相同的变量，所以把AC提出来，得：
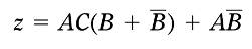
又因为
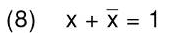
得
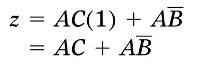
还可以再提一个A出来，得
例2
化简表达式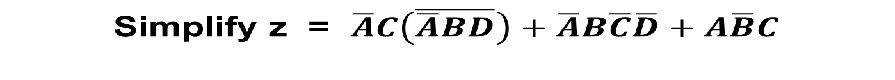
首先使用摩根定律得：
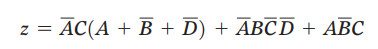
去括号：
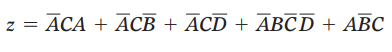
因为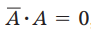
，消去第一项
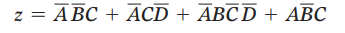
将共同的因子提取出来得：
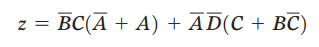
因为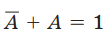
和定理15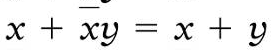
得：
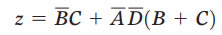
事实上这个也不是最简的形式，最简的形式是：
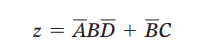
在上面的某个步骤中，错过了得到最简表达式的机会，后续内容中，将会讨论图形化简法，由它通常可得到最简与或表达式
例3
化简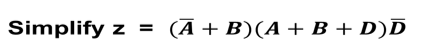
首先使用分配率将原表达式转换为与或表达式：
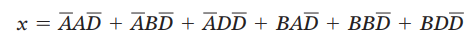
因为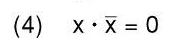
和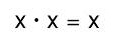
可消去1、3、6项，化简第五项，得：
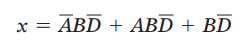
发现这三项都有共同的，将它提出来：
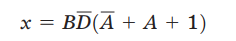
括号内的项永远等于1，最终结果为：
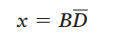
例4
简化如图所的电路
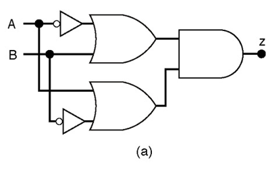
如图所示的电路的输出表达式是：
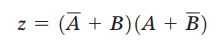
利用分配率求出与或表达式：
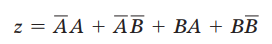
消去第一项和最后一项：
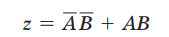
这个电路也可以用如下图所示的电路表示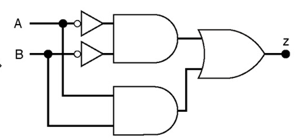
与原电路比较，可见这两个电路具有相同的门电路数目和连线，在这种情况下，化简过程产生了一个等效的电路但没有简化