关系代数
关系代数是一种过程化查询语言。它包括一个运算的集合,这些运以一个或两个关系为输入,产生一个新的关系作为结果。
关系代数基本运算有:选择、投影、并、集合差、笛卡尔积和更名
在基本运算以外,还有一些其他运算,即集合交、自然连接、赋值
基本运算
选择、投影和更名运算称为一元运算,因为它们对一个关系进行运算。
另外三个运算对两个关系进行运算,因而称为二元运算。
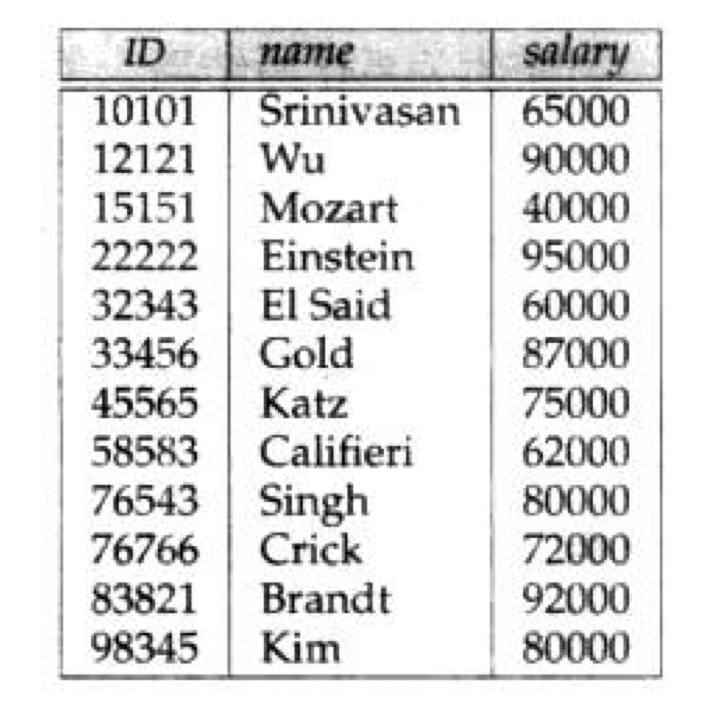
本文中涉及到的instructor的关系 如图:
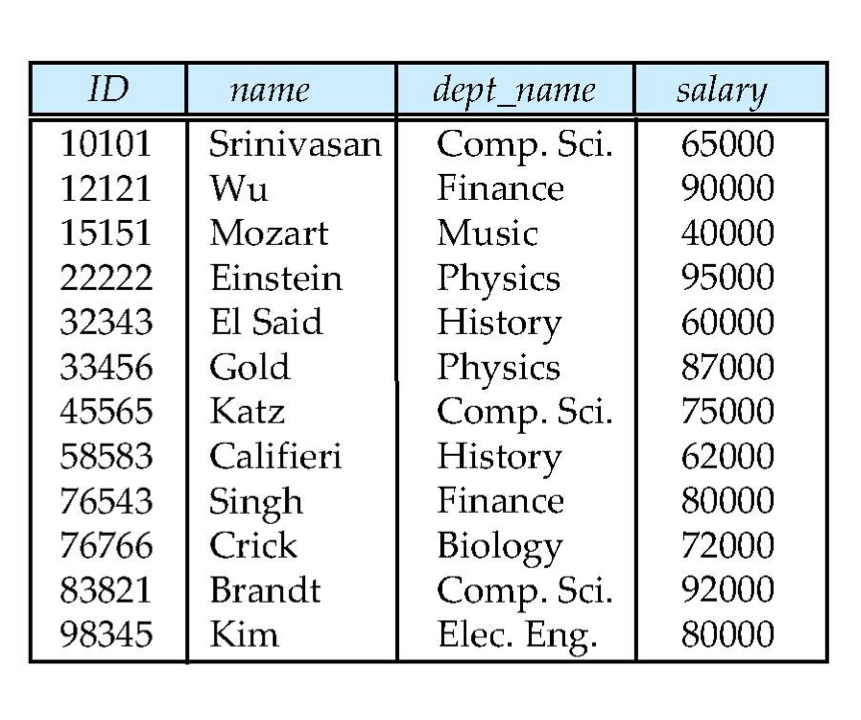
选择运算
选择(select)运算选出满足给定谓词的元组。
我们用小写希腊字母sigma(σ)来表示选择,而将谓词写作σ的下标。参数关系写在σ后的括号中
为了选择关系instructor中属于物理(Physics)系的那些元组,我们应该写作
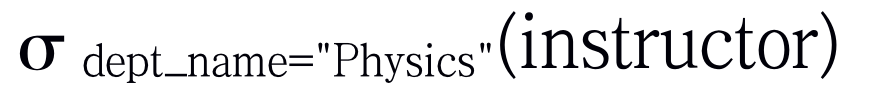
结果如图:

如果想找到工资额大于90000美元的所有元组:
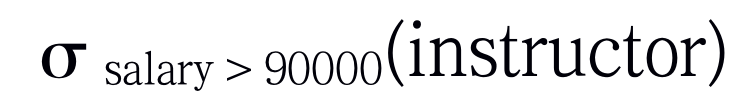
通常,我们允许在选择谓词中进行比较,使用的是= ≠ < ≤ > ≥
另外我们可以用连词and(∧)、or(∨)和not(¬)将多个谓词合并为一个较大的谓词
因此为了找到物理系中工资额大于90000的教师:

选择谓词中可以包括两个属性的比较。以department为例。
为了找到那些系名与楼名相同的系:

关系代数中的术语选择select与我们在sql中所使用的关键词select具有不一样的含义,这是因为历史原因造成的。在关系代数中,术语select对应于sql中使用的where
投影运算
假设我们想要列出所有教师的ID、name和salary,而不关心dept_name
投影(project)运算使得我们可以产生这样的关系
投影运算是一元运算,它返回作为参数的关系,但把某些属性排除在外
由于关系是一个集合,所以所有重复行均被去除。
投影用大写希腊字母pi(Π)表示,列举所有我们希望在结果中出现的属性作为Π的下标,作为参数的关系在跟随Π后的括号中。
因此我们可以写如下的查询来得到上述的教师列表:
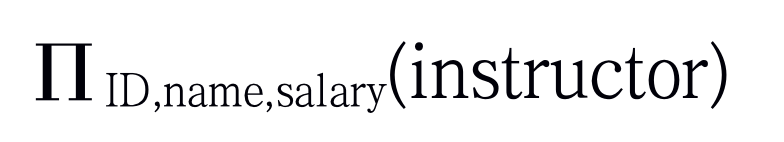
关系运算的组合
关系运算的结果自身也是一个关系,这一事实是非常重要的。
考虑一个更复杂的查询“找出物理系的所有教师的名字”,我们写作
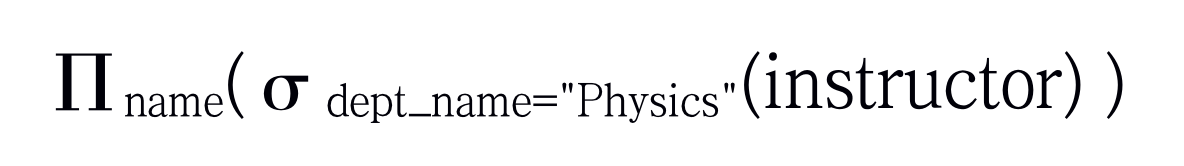
并运算
关系section如下图
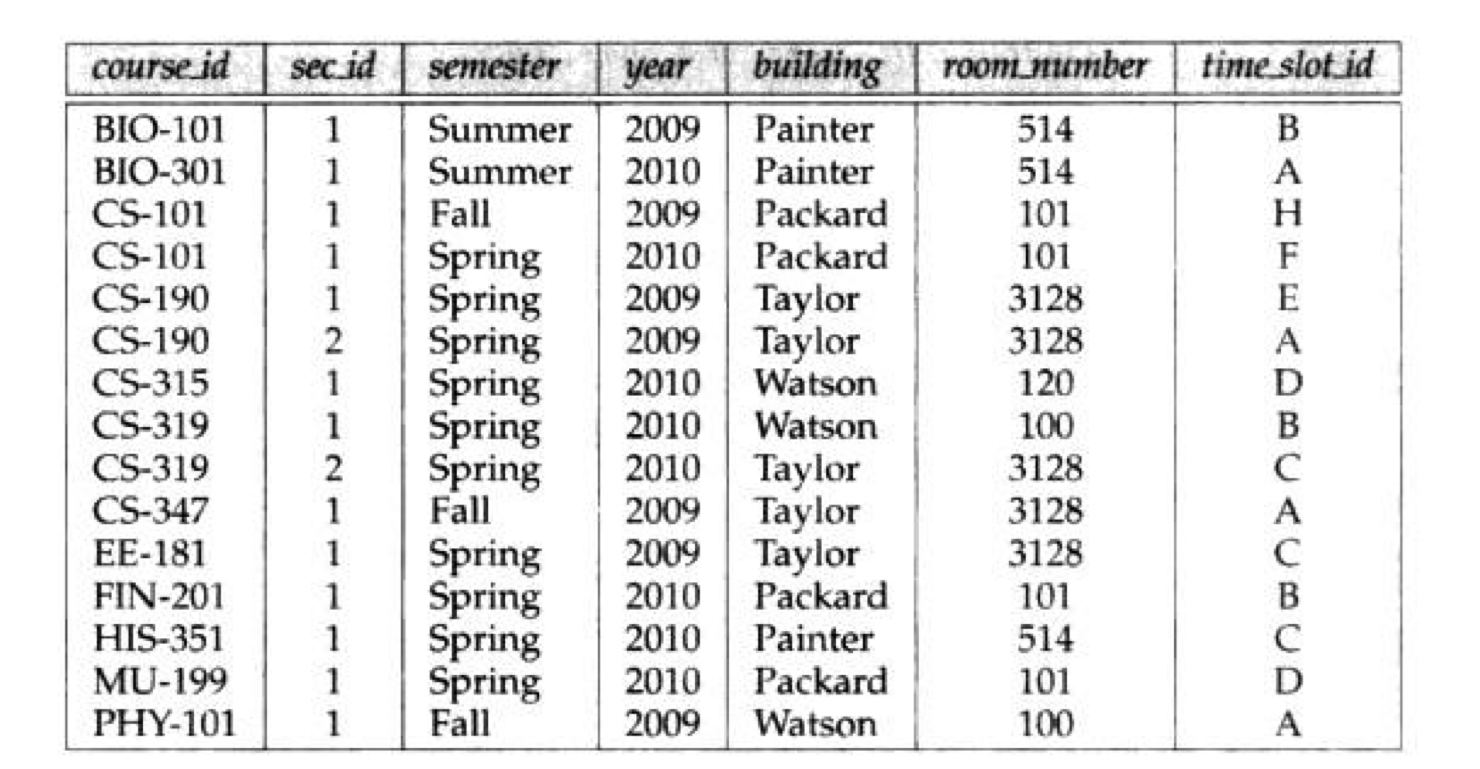
假设有一个查询,要找出开设在2009年秋季学期或者2010年春季学期或者这二者都开都所有课程的集合
为了找到2009年秋季学期开设的所有课程,我们可以这样写:
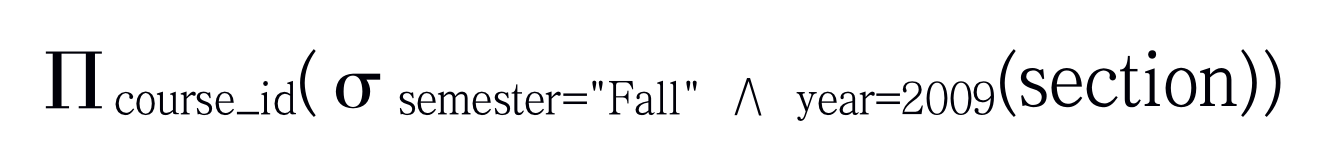
为了找出2010年春季学期开设的课程,可以这样写:
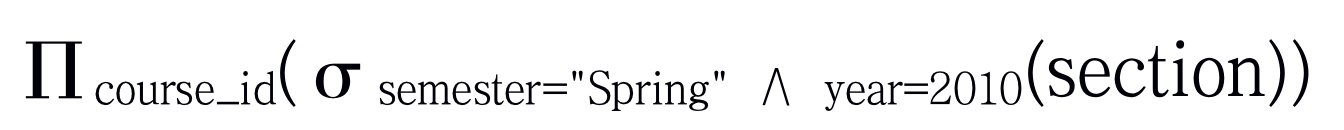
为了实现该查询,我们需要将上面这两个集合并(union)起来。我们通过二元运算并∪来表示。于是:
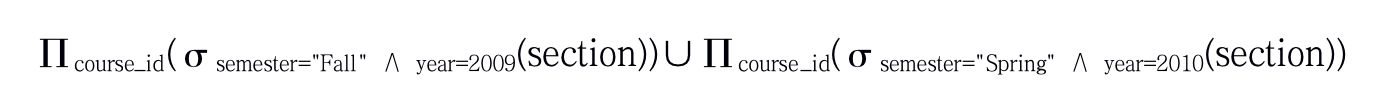
此查询的结果:

请注意 由于关系是集合,所以像CS-101这样在两个学期都开的重复值只留下了单个元组
可以看到,在我们的例子中,做并运算的两个集合都由course_id值构成。
概括地说,我们必须保证做并运算的关系是相容的,例如将instructor关系和student关系做并运算就没有意义。尽管两个关系都包含4个属性,但是二者在salary和tot_cred的域上是不同的。
在大多数情况下,这两个属性的并集是没有意义的。因此,要使并运算 r ∪ s有意义,我们要求以下两个条件同时成立
- 关系r和s必须是同元的,即它们的属性数目必须相同
- 对所有的i,r的第i个属性的域必须和s的第i个属性的域相同
集合差的运算
用 - 表示的集合差(set-different)运算使得我们可以找出在一个关系中而不在另外一关系中的那些元组。
表达式r-s的结果即一个包含所有在r中而不在s中的元组的关系
我们可以通过书写如下表达式来找出所有开设在2009年秋季学期但是在2010年春季学期不开的课程:
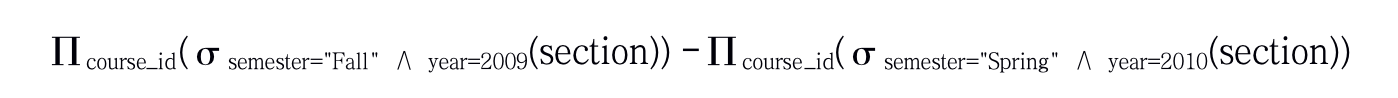
查询产生的关系如图所示:

就像并运算一样,我们必须保证集合差运算在相容的关系间进行。因此,为使集合差运算r - s 有意义。我们要求关系r和s是同元的,且对于所有的i,r的第i个属性的域与s的第i个属性的域都相同。
笛卡尔积运算
用 × 来表示笛卡尔积(cartesian-product)运算使得我们可以将任意两个关系的信息组合在一起。我们将关系r1和r2的笛卡尔积写作:r1 × r2
由于相同的属性名可能同时出现在r1和r2中,我们需要提出一个命名机制来区别这些属性。我们这里采用的方式是找到属性所来自的关系,把关系名称附加到该属性上
例如:r=instructor × teaches的关系模式为:
(instructor.ID,instructor.name,instructor.dept_name,instructor.salary
teaches.ID,teaches.course_id,teaches.sec_id,teaches.semester,teaches.year)
用这样的模式,我们可以区别instructor.ID 和 teaches.ID
对那些只在两个关系模式之一中出现的属性,我们通常省略其关系名的前缀,这样的简化不会导致任何歧义。
这样我们就可以把r的关系模式写作:
(instructor.ID,name,dept_name,salary
teaches.ID,course_id,sec_id,semester,year)
这个命名规则规定作为笛卡尔积运算参数的关系名字必须不同。这一规定有时会带来一些问题,例如当某个关系需要与自身做笛卡尔积时。后面将会介绍到通过更名运算来解决这些问题。
我们已经知道r =instructor × teaches的关系模式,那么到底哪些元组会出现在r中呢?
每一个可能的元组对都形成r的一个元组,元组对中一个来自关系instructor而另一个来自关系teaches。因此如下图所示,下图只显示来构成r的部分元组
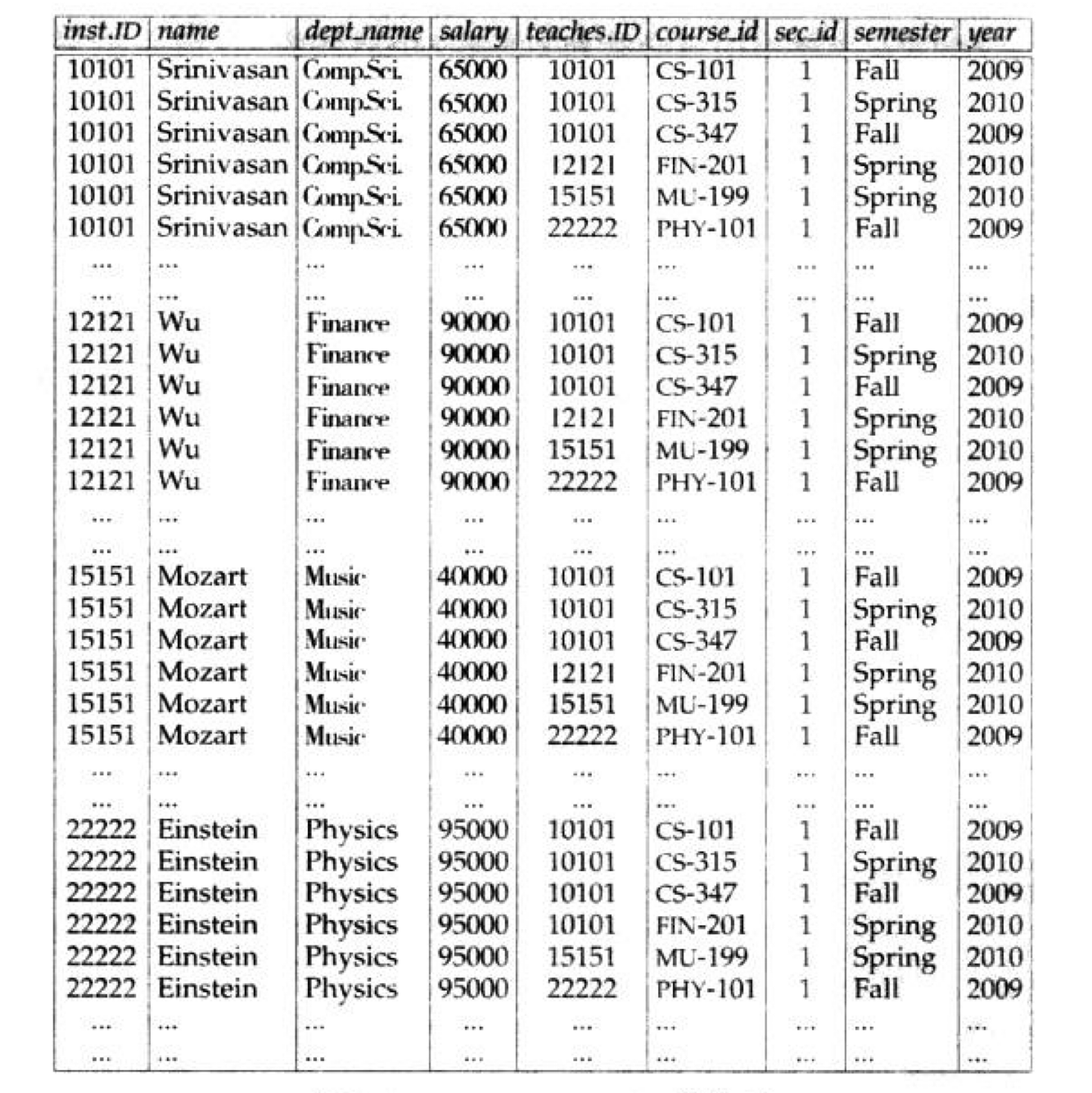
假设instructor中有n1个元组,teaches中有n2个元组,那么我们可以有n1 × n2种方式来选择元组对————每个关系中选出一个元组。因此r1中有n1×n2个元组
假设我们希望找出物理系的所有教师,以及它们教授的所有课程。为了实现这一要求,我们同时需要关系instructor和关系teaches中的信息。如果我们写:

结果就是如图的关系:
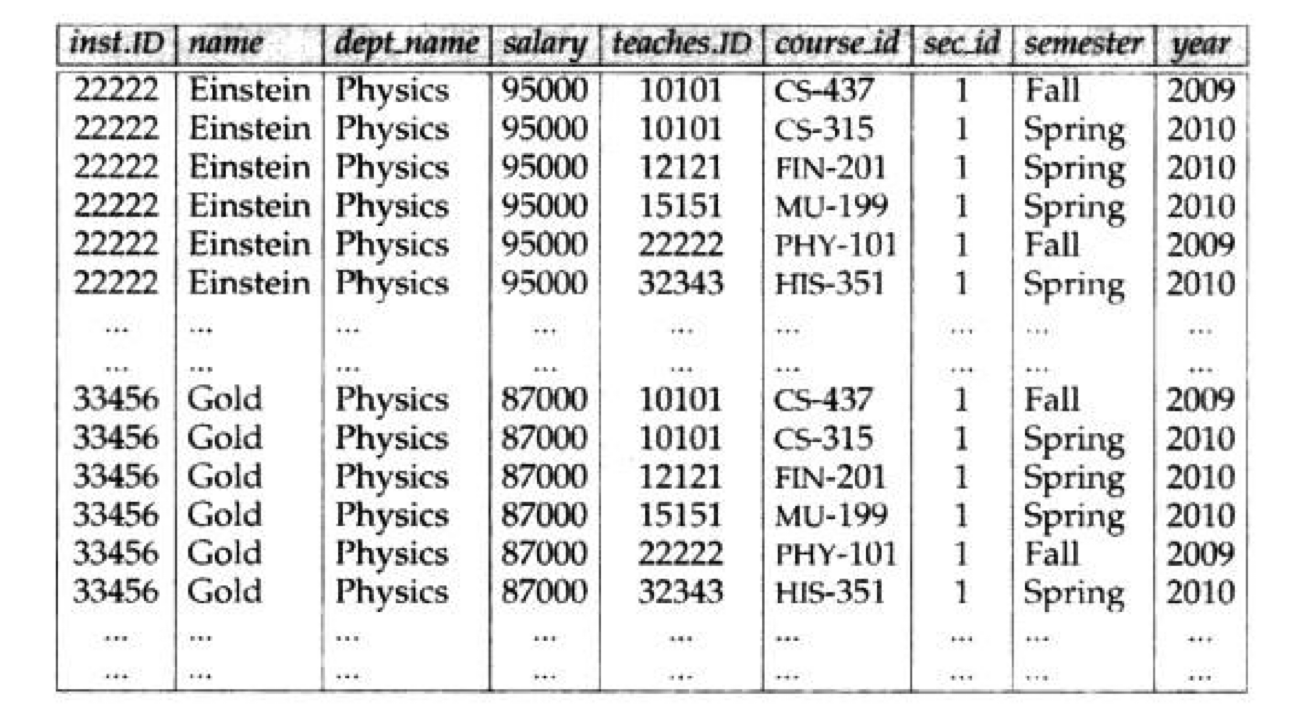
这里我们得到的关系中只包含物理系的教师,然而course_id列却可能包含并非这些教师所教授的课程(笛卡尔积中保留了所有可能的由一个来自instructor的元组和一个来自teaches的元组构成的元组对)
由于笛卡尔运算将instructor中的每个元组同teaches中的每个元组进行联系,所以我们可以确定,如果一名教师来自物理系并教授某门课程(在关系teaches中有对应的元组)那么必定存在某个元组,它包含该教师的名字,并且满足instructor.ID =teaches.ID 因此,如果我们用
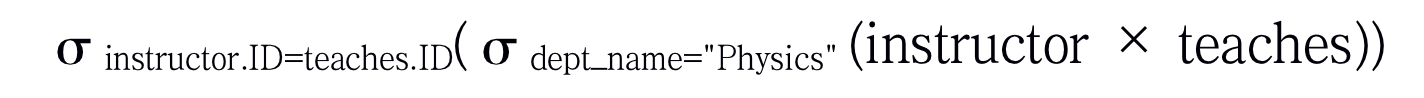
就可以得到在instructor × teaches中那些只与物理系教师以及他们所教课程相关的元组
最后,由于我们只需要物理系教师的名字,以及他们所教的课程的course_id我们进行投影:
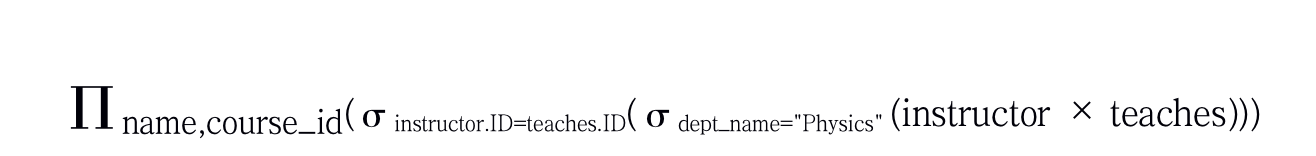
查询的结果:

需要注意,用关系代数表达查询的方法并不唯一。考虑下面的这个查询:
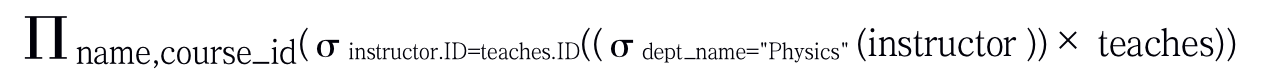
这两个查询的细微差别:
上面的查询是对instructor进行选择运算,把dept_name限制为Physics。之后再进行笛卡尔积。这是等价的,可以得到相同的结果
更名运算
关系代数表达式的结果没有可供我们引用的名字,这一点与数据库中的关系有所不同。如果能给它们附上名字那将是十分有用的
我们可以通过小写希腊字母rho(ρ)表示的更名(rename)运算来完成这一任务
对给定关系代数表达式E,表达式
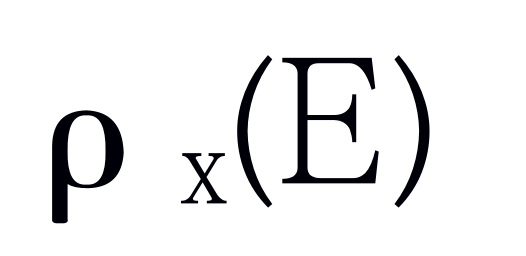
返回表达式E的结果,并把名字x赋给了它
对于一个关系r来说,它自身被认为是一个关系代数表达式。因此,我们也可以将更名运算运用于关系r,这样可得到具有新名字的一个相同的关系。
更名运算的另一形式如下。假设关系代数表达式E是n元的,则表达式:
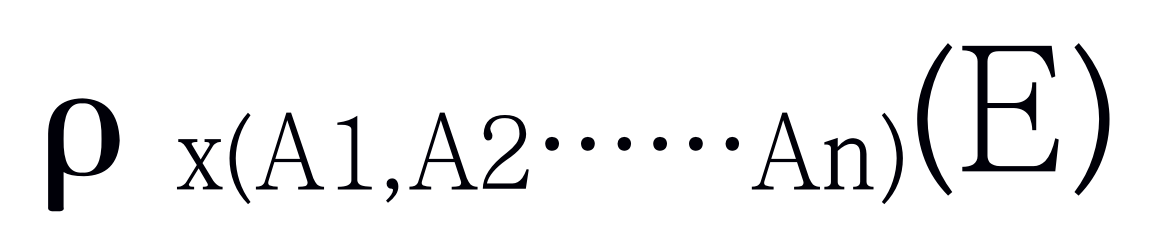
返回表达式E的结果,并赋予它名字x,同时将各个属性更名为A1,A2…… An
我们以查询 找出大学里的最高工资 作为例子来演示关系的更名运算。
我们的策略是:首先计算出一个由非最高工资组成的临时关系,然后计算关系

和刚才算出的临时关系之间的合差,从而得到结果
为了计算该临时关系,我们需要比较所有工资的值
要做这样的比较,可以通过计算笛卡尔积 instructor × instructor 并构造一个选择来比较任意两个出现在同一元组中的工资。
我们的首要任务是设计一种机制来区别两个salary属性,我们将使用更名运算来改变其中一个对教师关系进行引用的名字;这样我们就可以无歧义得两次引用这个关系
现在可以把非最高工资构成的临时关系写作:
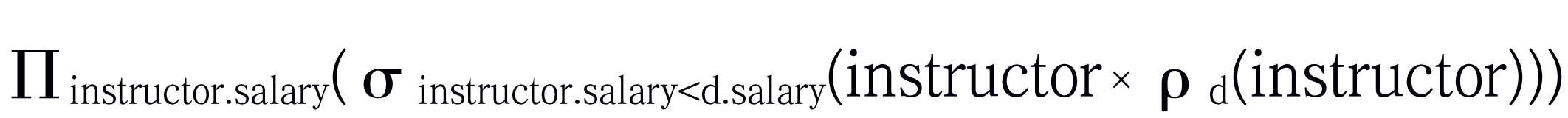
通过这一表达式可以得到instructor中满足如下条件的那些工资:在关系instructor(更名为d)中还存在比它更高的工资。结果中包含了除最高工资以外的所有工资。
查询大学里的最高工资的查询可写作:

结果如下:
